Courtesy : Bachelor of Science Mathematics- PCM (Physics, Chemistry, Mathematics) Alumni
Training and practice
Education
Main article: Mathematics education
Mathematics has a remarkable ability to cross cultural boundaries and time periods. As a human activity, the practice of mathematics has a social side, which includes education, careers, recognition, popularization, and so on. In education, mathematics is a core part of the curriculum and forms an important element of the STEM academic disciplines. Prominent careers for professional mathematicians include math teacher or professor, statistician, actuary, financial analyst, economist, accountant, commodity trader, or computer consultant. # ISO certification in India
Archaeological evidence shows that instruction in mathematics occurred as early as the second millennium BCE in ancient Babylonia. Comparable evidence has been unearthed for scribal mathematics training in the ancient Near East and then for the Greco-Roman world starting around 300 BCE. The oldest known mathematics textbook is the Rhind papyrus, dated from circa 1650 BCE in Eygpt. Due to a scarcity of books, mathematical teachings in ancient India were communicated using memorized oral tradition since the Vedic period (c. 1500 – c. 500 BCE). In Imperial China during the Tang dynasty (618–907 CE), a mathematics curriculum was adopted for the civil service exam to join the state bureaucracy.
Following the Dark Ages, mathematics education in Europe was provided by religious schools as part of the Quadrivium. Formal instruction in pedagogy began with Jesuit schools in the 16th and 17th century. Most mathematical curriculum remained at a basic and practical level until the nineteenth century, when it began to flourish in France and Germany. The oldest journal addressing instruction in mathematics was L’Enseignement Mathématique, which began publication in 1899. The Western advancements in science and technology led to the establishment of centralized education systems in many nation-states, with mathematics as a core component—initially for its military applications. While the content of courses varies, in the present day nearly all countries teach mathematics to students for significant amounts of time. # ISO certification in India
During school, mathematical capabilities and positive expectations have a strong association with career interest in the field. Extrinsic factors such as feedback motivation by teachers, parents, and peer groups can influence the level of interest in mathematics. Some students studying math may develop an apprehension or fear about their performance in the subject. This is known as math anxiety or math phobia, and is considered the most prominent of the disorders impacting academic performance. Math anxiety can develop due to various factors such as parental and teacher attitudes, social stereotypes, and personal traits. Help to counteract the anxiety can come from changes in instructional approaches, by interactions with parents and teachers, and by tailored treatments for the individual. # ISO certification in India

Psychology (aesthetic, creativity and intuition)
The validity of a mathematical theorem relies only on the rigor of its proof, which could theoretically be done automatically by a computer program. This does not mean that there is no place for creativity in a mathematical work. On the contrary, many important mathematical results (theorems) are solutions of problems that other mathematicians failed to solve, and the invention of a way for solving them may be a fundamental way of the solving process. An extreme example is Apery’s theorem: Roger Apery provided only the ideas for a proof, and the formal proof was given only several months later by three other mathematicians. # ISO certification in India
Creativity and rigor are not the only psychological aspects of the activity of mathematicians. Some mathematicians can see their activity as a game, more specifically as solving puzzles. This aspect of mathematical activity is emphasized in recreational mathematics.
Mathematicians can find an aesthetic value to mathematics. Like beauty, it is hard to define, it is commonly related to elegance, which involves qualities like simplicity, symmetry, completeness, and generality. G. H. Hardy in A Mathematician’s Apology expressed the belief that the aesthetic considerations are, in themselves, sufficient to justify the study of pure mathematics. He also identified other criteria such as significance, unexpectedness, and inevitability, which contribute to mathematical aesthetic. Paul Erdős expressed this sentiment more ironically by speaking of “The Book”, a supposed divine collection of the most beautiful proofs. The 1998 book Proofs from THE BOOK, inspired by Erdős, is a collection of particularly succinct and revelatory mathematical arguments. Some examples of particularly elegant results included are Euclid’s proof that there are infinitely many prime numbers and the fast Fourier transform for harmonic analysis. # ISO certification in India
Some feel that to consider mathematics a science is to downplay its artistry and history in the seven traditional liberal arts. One way this difference of viewpoint plays out is in the philosophical debate as to whether mathematical results are created (as in art) or discovered (as in science). The popularity of recreational mathematics is another sign of the pleasure many find in solving mathematical questions.
In the 20th century, the mathematician L. E. J. Brouwer even initiated a philosophical perspective known as intuitionism, which primarily identifies mathematics with certain creative processes in the mind. Intuitionism is in turn one flavor of a stance known as constructivism, which only considers a mathematical object valid if it can be directly constructed, not merely guaranteed by logic indirectly. This leads committed constructivists to reject certain results, particularly arguments like existential proofs based on the law of excluded middle. # ISO certification in India
In the end, neither constructivism nor intuitionism displaced classical mathematics or achieved mainstream acceptance. However, these programs have motivated specific developments, such as intuitionistic logic and other foundational insights, which are appreciated in their own right.
Cultural impact
Artistic expression

Cover page of Traité de l’harmonie réduite à ses principes naturels by Jean-Philippe Rameau
Notes that sound well together to a Western ear are sounds whose fundamental frequencies of vibration are in simple ratios. For example, an octave doubles frequency and a perfect fifth multiplies it by {\displaystyle {\frac {3}{2}}}
This link between frequencies and harmony was notably discussed in Traité de l’harmonie réduite à ses principes naturels by Jean-Philippe Rameau[, a French baroque composer and music theoretician. It rests in part on the analysis of harmonics (noted 2 to 15 in the following figure) of a fundamental Do (noted 1); the first harmonics and their octaves sound well together. # ISO certification in India
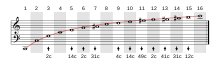
Harmonics on a staff
The curve traced in red has a logarithmic shape reflects the following two phenomena:
- The representation of sound’s pitch by our auditive system, which is proportional to the logarithm of the sound’s frequency. (Twice the frequency always corresponds to the same “sound distance”, called an octave.)
- Harmonic frequencies, which are integer multiples of the fundamental frequency.
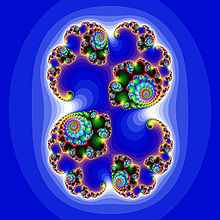
Fractal with a scaling symmetry and a central symmetry
Western people associate a certain beauty to symmetric figures. A symmetry of a geometric figure is, intuitively, the existence of a motif of the figure which repeats according to a precise rule. Mathematically, a symmetry is the existence of a nontrivial action of a group, often by isometry (i.e. which preserves distances within the figure). In other terms, the intuition of a rule is mathematically realized by the fact that a group acts on the figure, and the feeling that a rule regulates the symmetry is precisely due to the algebraic structure of the group.
For example, the group underlying mirror symmetry is the cyclic group of two elements, {\displaystyle \mathbb {Z} /2\mathbb {Z} }



